|
:: 게시판
:: 이전 게시판
|
- 모두가 건전하게 즐길 수 있는 유머글을 올려주세요.
- 유게에서는 정치/종교 관련 등 논란성 글 및 개인 비방은 금지되어 있습니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
23/04/27 17:12
(수정됨) 틀린 말이 아니라고 볼 수도 있기는 하겠지만,
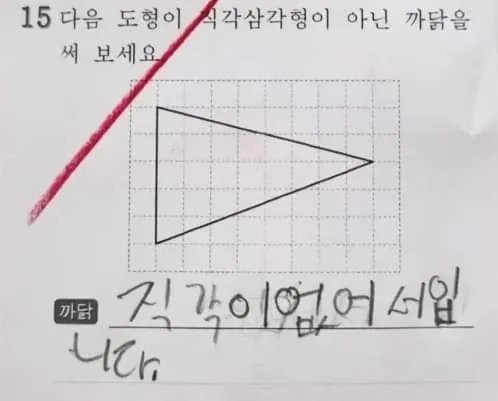
이게 경우에 따라서는 '까닭을 설명한 것'이 아니고 [동어반복을 한 것]이라고 판단될 수도 있겠네요. '특정 삼각형이 직각삼각형이 아니다 = 특정 삼각형에 직각이 없다'이니까... 까닭을 설명하려면 [왜 직각이 없다고 판단했는가] 까지는 가야겠죠. 직각이 없음을 판단하기 위해 격자가 제공되었을 것이고요. '눈으로 봐서 직각이 없다고 판단했다' 라면, 수학적인 답변은 아닐 겁니다.
23/04/27 17:15
사실 저 문제와 연관된 가장 중요한 지식은 직각삼각형의 정의 아닌가요? 그 관점에서 보면 답이 타당합니다.
차이를 비교하기 위해 예각삼각형을 생각하면 예각이 없어서는 틀린 답이 되는 거고, 저 말을 썼다는 건 곧 직각삼각형은 직각이 하나만 있으면 된다는 사실을 안다는 거니까요
23/04/27 17:40
그렇죠. 그러니까 예각삼각형이 아닌 이유를 써라! 에 예각이 없어서 라고 답하면 틀리잖아요. 예각이 아닌 각이 있어서 라고 써야 맞고요. 그러니까 a삼각형이 아닌 이유를 써라! 라고 했을 때 a가 없어서! 라는 답은 자명한 게 아니라는 말입니다.
따라서 저 학생은 직각삼각형의 정의를 안다고 볼 수 있고, 그러니까 정답인 거죠.
23/04/27 17:47
무슨 의도인지는 알겠지만 비유가 조금 다르긴 하네요. 예각삼각형의 정의는 예각이 있는 삼각형이 아니라 모든 각이 예각인 삼각형이니까요.
예각이 없다고 말하면 당연히 틀리죠...최소 두 각은 예각이니까...둔각삼각형 쪽이 좀 더 말씀하신 의도에 맞겠네요.
23/04/27 17:51
저도 둔각 삼각형을 생각했는데,
둔각 삼각형의 경우는 사실 본문 케이스와 아예 똑같아져버려서 논의의 실익이 없는 것 같습니다.
23/04/27 17:49
비유클리드 기하학에서 예각이 없는 삼각형은 없으니까,
'예각이 없어서'라고 말하면 예각삼각형의 정의와 무관하게 무조건 오답이 되는 겁니다. 어떤 삼각형이든, 주어진 삼각형에는 반드시 예각이 있을테니까요. 삼각형에 멀쩡히 예각이 있는데 '예각이 없다'고 하면 당연히 틀리죠.
23/04/27 18:06
제 댓글을 다시 읽어봐주시면, 그걸 제가 알고 있기 때문에 그런 예시를 굳이 든 겁니다. 물론 여러 분께서 이렇게 말씀하시는 걸 보면 제 서술이 매우 불명확했던 모양인데… 일단 제가 말을 잘 못해서 그렇지 잘못된 말을 한 건 아닙니다.
23/04/27 17:45
그래서 저는 저걸 정답처리를 하던지, 아니면 문제에서 다음 유클리드평면의 직각 격자상에 있는 다각형이 직각삼각형과 동치로 볼 수 없는 이유를 써라... 라고 하던지... 했어야 됐을것같네요 -_-
23/04/27 17:12
피타고라스의 정리를 배우는 시기라면
짧은 두 변의 제곱의 합이 긴 변의 제곱과 같지 않기 때문 이라고 적어야 될 거 같긴 하네요.
23/04/27 17:17
왜 직각이 없다고 판단했는지까지를 써주는 게 답이겠죠. 그걸 위해 격자들이 제공되었을 것이고요
- 격자 구조에 기초해서, 각각의 각도들 중 직각에 해당하는 각도가 없는 이유를 설명하든지, - 아니면 격자 구조에 기초해서 구해진 3개의 변들의 길이의 제곱값에 기초해서 '두 변의 길이의 합이 나머지 한 변의 길이의 합이 될 수 없다'는 것을 설명하든지요.
23/04/27 17:22
그렇게까지 가면, 저게 유클리드 평면이라는 보장도 없어서... 더더욱 본문의 답으로는 까닭이 설명이 안되는 것 같기도 하고요...?
23/04/27 17:25
아하... 제가 학년별 교육과정의 변수를 생각하지 못했네요.
다만, 피타고라스 정리가 나오기 전이라면 후자로는 설명을 못하더라도 전자로는 설명을 할 수 있지 않은가요? 세 각이 모두 예각이라고 할 수 있을 것도 같은데요.
23/04/27 17:35
피타고라스는 아직 배우기 한참 전이고, (세 내각 중)한 각이 직각인 삼각형을 직각 삼각형이라고 배웠을텐데.. 저 학생이 쓴답은 정확히 대우와 일치하는것으로 보이구요.
그걸 떠나서 문제 자체가 논란일 수밖에 없도록 츌제한게 가장 문제 인덧 같은데 저 빨간색 틀림 표시가 너무 매몰차 보이네요.
23/04/27 17:33
왜 직각이 없는지 설명하는게 모눈을 이용하면 초등학생 수준에서도 가능할 겁니다.
모눈이 직각이란거랑 모눈 반갈하면 나오는 각이 직각의 반이라는것 정도는 직각삼각형 배우는 수준에서는 이미 가르쳐 줬을 테니까요. 왼쪽 두개는 아예 모눈과 겹쳐있으니 그냥 "직각보다 크기가 작다"고 하면 OK일 거고, 오른쪽도 꼭지점 끼고 >모양으로 모눈 이으면 그게 직각이니 비교했을때 더 작다고 하면 끝일 것 같습니다.
23/04/27 17:18
직각삼각형의 정의에 대해 배웠을거고 (예를들면 만나는 두 선의 각이 직각인 삼각형)이 시험문제의 목적은 그 정의에 대해 쓰라는 것일테니
단순히 "직각이 없어서"는 틀린거겠죠. 정의에 대해 바르게 알고 있는지를 물어봤는데 제대로 기술하지 못했으니까요.
23/04/27 17:22
위에 비슷한 댓글을 달았는데, 결국 시험문제에서 이유를 쓰라는 건 가장 ‘비-자명’한 사실을 쓰라는 것이라고 봅니다. 논리적으로만 보면 뭘 설명할 게 없죠. 사실->사실에는 이유가 없으니, 증명이 필요한 부분이 어디인지는 아주 엄격히 말하면 ’사회적‘인 합의입니다.
그런데 저는 저기서 가장 ’비-자명‘한 사실은 직각삼각형의 정의라고 생각합니다. 따라서 저 답은 말이 되는데, 예를 들어 예각삼각형이 아닌 이유를 쓰시오, 라고 하면 예각이 없어서는 틀린 답이죠. 그러니까 저 답을 쓰려면 직각삼각형의 정의를 알아야만 합니다. 따라서 저는 꽤 괜찮은 답이라고 생각해요.
23/04/27 17:27
음.. 맞습니다 말씀하시고자 하는 바는 저도 동의합니다.
다만 제가 틀렸다고 말씀드린 기준은 [저 시험문제를 푸는 대상은 누구인가 & 시험의 출제 의도는 무엇인가] 입니다. 만약 저 시험 문제를 중학교나 고등학교, 혹은 성인들을 대상으로 출제했다고 하면 말씀하신 부분에 대해 저도 완전히 동의했을텐데요. 이 문제는 아무리봐도 직각삼각형에 대해 처음 배우는 초등학생 3~4학년 정도의 학생들을 대상으로 하고 있을거라고 봅니다. 그렇다면 이 시험의 출제 의도는 분명히 직각삼각형의 [두선의 각이 직각인 삼각형]이라는 정의에 대해 물었을 거라고 짐작합니다. 앞에서 가르친 수업의 내용을 충실히 이행했는지 물어보는 의도였을 거구요. 그런 관점에서 보았을 때 저는 저 답이 틀렸다고 생각합니다.
23/04/27 17:36
네, 그렇게 생각하면 좋은 답이 아닙니다.
다만 제가 생각하기에 그렇게 볼 때 저 이상을 요구하기 애매한 부분은, 그럼 저 오른쪽의 각이 직각이 아닌 건 초등 교육과정 기준으로 어떻게 설명할 것이냐는 문제입니다. 격자와 평행하지 않은 두 선이 만드는 각이 직각일 조건에 대해서도 생각해야 하는데, 초3-4 수준에서는 눈으로 보기에 직각이 아니라서 이상을 말할 수 없거든요. 그럼 초3-4 기준으로도 가장 비-자명한 사실은 직각삼각형의 정의고, 이때 ‘가장’의 의미는 성인의 지식수준에서와는 좀 다른데, 사실 쓸 말이 저것밖에 없어서…이기도 합니다. 처음 쓸 때랑 논리가 달라지긴 했는데, 아무튼 저는 저걸 틀렸다고 하는 건 교사가 너무하다고 생각해서… 조금 억지를 부려봅니다.
23/04/27 17:31
바로 맞습니다. [직각을 가진 삼각혀여]이니까요.
이 문제의 출제 의도는 직각이 있다 없다를 찾는게 아니라, 직각에 대해 잘 알고 있는지 확인하는 거라고 봅니다. 그런 의도에서 직각이 무엇인지를 더 잘 서술했어야하지 않을까 싶습니다. 물론, 그전에 문제가 좀 더 명확했어야 하는 점을 지적해야 할 것 같구요
23/04/27 17:35
근데 직각이 뭔지 아니까 직각이 없다고 하지 않았을까요?
두 선분이 만나서 이루는 각이 90도인 내각이 없어서 라고 썼다면, 선분이 뭔지, 각이 뭔지도 자세하게 설명해야 하나요? 그렇게 나가면 끝도 없지 않을까요?
23/04/27 17:37
크크크 그럴수도 있겠죠. 생각해보니 그렇네요. 초등학생이 갸우뚱하면서, 아니 직각이 없는데? 하면서 무의식중에 직각이 없음으로 써버릴수도 있을 것 같긴하네요.
23/04/27 17:54
아래 인용한 채점 취지에 따르면, 말씀하신 이유가 맞는 것 같네요.
https://cdn.pgr21.com./humor/478537#7610486
23/04/27 17:23
초등 3학년 수준에서 정답 맞습니다. 틀렸다고 한 채점한 교사 오류입니다. 요즘 교사별 펑가라 이런 문제에서 담임교사가 강조한 내용이 따로 있을 지는 모르지만, 국정교과서 상 저게 정답입니다.
23/04/27 17:23
성인한테 풀라고 내놓은 문제였으면 모든 문제에는 출제자의 의도라는 게 있으니 답변자가 알잘딱을 했어야지 하는 게 맞을 수 있는데,
아이한테 풀라고 내놓은 문제니 질문을 좀 더 잘하는 게 좋았다고 보입니다.
23/04/27 17:25
직각 삼각형의 정의는 세 내각 중 하나가 직각인 삼각형 아닌가요?
그럼 직각이 없어서 직각 삼각형이 아니다 라는건 직각 삼각형의 정의에서 나온 훌륭한 답인 것 같습니다. 세 내각 중 하나의 각이 직각이라면, 직각삼각형이다. 직각삼각형이 아니라면, 세 내각 중 직각인 각이 없기 때문이다. 대우 명제로 정확하게 설명한거죠.
23/04/27 17:36
직각삼각형을 처음 배우는 초등3학년에서 정의는 [직각삼각형=한 각이 직각인 삼각형] 입니다.
담임교사가 반례를 들어서 어떤 삼각형이 직각삼각형이 아닌 까닭으로 "직각삼각형은 한각이라도 직각이어야 하지만, 세 각이 모두 직각이 아니기 때문이다" 라고 설명했다 하더라도, 이 문제에서 답으로 제시한 "직각이 없기 때문이다" 는 정답으로 해야 합니다. 만약 오답으로 채점한 이유로 사전에 "직각이 없기 때문이다"라고 하면 틀리게 할 것이다라고 명시했더라도 교사 채점 잘못입니다.
23/04/27 17:38
공대 출신이 봐도 이건 정답인데요?? 직각이 없으니 직각삼각형이 아닌데...
설마 초등 문제에 피타고라스 정리 어쩌고 하라는 얘기는 아니겠죠?
23/04/27 17:43
(사실인지는 모르겠지만) 아래 엠팍 게시물에 [저 답이 오답처리된 이유]가 인용되어 있네요.
https://mlbpark.donga.com/mp/b.php?m=user&p=1&b=bullpen&id=202304240080411571
23/04/27 17:46
(수정됨) 엠팍에 인용된 [본문의 답이 오답처리된 이유] 옮겨적습니다
----------------------------------------- "그래서 정답을 적을 때는 직각이 없어서, 비뚤어져서 이렇게 적을 것이 아니라 "[직각삼각형은 한 각이 직각입니다. 이 삼각형에는 직각이 없기 때문에 직각삼각형이 아닙니다]"라고 적어야 합니다. 1. 직각삼각형의 정의를 알고 있는지 2. 주어진 도형이 아닌 이유를 썼는지"
23/04/27 17:47
이게 이유라면... 음...
교과과정상 학생 평가 기준은 잘 모르겠지만 [수학적인 이유로는 틀리지 않은 답]이 되는 것 같습니다.
23/04/27 20:15
이런 답을 원했다면
문제가 [직각 삼각형에 대해서 설명하고 아래 그림이 직각 삼각형이 아닌 이유를 쓰시오] 가 되야 된다고 생각합니다
23/04/27 17:51
저게 뭐 중요한 시험에 출제된 문제였다면 논란이 일어도 할 말 없겠지만,
논리적 사고를 키우기 위한 학습의 과정이라고 생각한다면 마냥 '저건 아니지' 할 수 있는 건 아닌 듯 하네요 흐흐
23/04/27 17:47
(수정됨) 다시 보니 이게 참 직각삼각형이라는 녀석이 특수한 사례라서 생긴 일인 거 같습니다.
5cm 3cm 4cm짜리 삼각형보고 이등변삼각형 아닌 이유 설명하라고 했을 때 길이가 같은 변이 없어서요 라고 하면 이건 논란의 여지가 없는 100% 정답이거든요. 다르다는 게 확 드러나니까요 근데 직각삼각형은 결국 직각이 뭔지 모르는 학생 입장에서도 직각삼각형이 뭔 삼각형이다 라고 들은 게 있으면 저 삼각형이 직각삼각형인지 아닌지 모르겠지만 일단 이렇게 쓰면 되겠지 하는 마음으로 때려맞히기가 가능해집니다. 저게 엄정한 시험이라면 그럼에도 불구하고 정답처리를 해줘야겠지만 가르치는 과정이라면... 학생이 제대로 모르고 넘어갈 수 있게 되는 거죠 저라면 틀렸다 하기보단 일단은 맞다고 하고 학생에게 이유를 물어보거나 하는 코멘트를 달아줬을 거 같습니다
23/04/27 17:50
제일 바보같은 문제, 나쁜 문제가 저런거죠.
'지금 니가 배우는 과정에선 정답이 아니라 xxx라는 이유를 대야 해' 또는 '출제의도는 xx였으니까 yy라는 답을 써야해' 라는 식으로 말하면서 틀렸다고 채점하는건데... 그럴거면 출제의도를 명확하게 문제에서 제시했어야죠.
23/04/27 17:54
오매..나중에 딸아이 커서 저런거 알려달라고 해서 저렇게 알려줬는데 선생님이 틀렸대ㅠㅠ 하면서 집에오면 어찌해야쓰까요..가뜩이나 산수, 수학 무서운데 ㅠㅠ
23/04/27 18:06
제가 보기엔 저건 선생님 재량에 따라 맞는다고 할 수도, 틀린다고 할 수도 있을 것 같습니다. 개인적으로는 맞게 해 주는 것이 합당해 보입니다만......
어렵게 생각할 필요 없이 초등학교 수준에서의 직각삼각형의 정의라는 것이 '세 각 중 한 각이 직각인 삼각형' 정도일 건데, 그렇다면 저 문제의 정답은 '세 각 중 직각인 각이 없으므로' 혹은 '세 각이 모두 직각이 아니므로' 가 될 겁니다. 앞에 '세 각 중에서', '세 각이' 라는 말을 쓰면 더 정확한 답이 되긴 하겠지만, 저것만으로도 답이 안 될 이유는 없어 보이는데요. 모눈종이는 세 각이 모두 직각이 아니라는 걸 나타내기 위함인 것 같고요.
23/04/27 18:40
저도 저 답을 오답 처리 할 거였다면 문제에서 의도를 명확하게 밝혔어야 어쩌고 저쩌고 쓰다가 혹시 이 경우인가 싶어서 지웠네요...
23/04/27 18:32
(수정됨) 만약 삼각형의 세 내각중 을 앞에 붙였다면 무조건 정답이어야 하고 그런 내용이 빠졌으므로 오답처리인 것 같습니다. 소위 말해 주어 내지는 어디에서가 빠진 형태의 비문에 가까우니까요. 우기자면 격자에는 직각이 있으니깐... 그런데 또 국어적으로 보면 질문에 삼각형이 들어갔으니 당연히 답변에도 삼각형에 관한 이야기일테니까 생략도 가능한 것이고...... 암튼 좋은 문제는 아닌 것 같습니다.
23/04/27 18:36
이거와는 조금 다를 수 있는데
문득 제 대학교 시험 때 문제 다 풀고 답을 적어서 제출했더니 반정답 처리된 기억이 나네요(컴퓨터공학 3학년) 이유는 풀이과정이 없어서 흑흑 다음부터는 풀이과정도 다 남겼습니다..
23/04/27 19:31
정답처리 해줘야 한다고 봅니다.
정의와 관련해서 오답처리 하려면 '직각삼각형이 아닌 까닭을 직각삼각형 정의와 관련해서 설명하시오'라는 문구가 있어야 합니다.
23/04/27 20:34
뭐 저나이때에는 충분히 맞는말만 하면 되는거아냐? 생각할만하죠
의도와 맥락에 맞는형태의 답변을 내놓는것의 필요성을 크게 느끼려면 최소한 대학생까진 가야할테니 그리고 제눈에도 굳이 저걸 오답으로 처리해야하나 싶기도하고요
23/04/27 21:14
애초에 문제가 오류입니다. 직각 삼각형이 아닌 이유를 적으라는건데 직각 삼각형이 아닌걸 알려면 직각이라는 개념과 삼각형이라는 개념을 알아야합니다. 그럼 전제조건으로 직각삼각형이라는걸 출제자도 알고 수험자도 알고 있다. 이걸 깔고 들어가는건데 이 상황에서 [직각이 없으니 직각삼각형이 아니다]이게 왜 오답이 되는겁니까? 직각이라는걸 구구절절히 설명할 필요가 없는데요.
그래서 의도 자체는 알겠는데 문제 자체가 오류입니다. 직각에 대한 정의와 직각 삼각형이 아닌 이유를 적으시오 라고 적었어야 저걸 오답처리 할수 있는겁니다.
23/04/28 13:20
학생이 틀렸다는 가정을 좀 파보면
뭐 수학자가 꿈이 아니고서야 이 정도 까지 초딩수준에서 할필요까지야... 직각 삼각형에서도 직각이 없는 부분이 있습니다. 그니깐 모든 각이 예각이다 모든 각이 직각이 아니다가 정답같아보입니다. 우겨보면 직각이 없진 않아요 모눈종이에 이미 직각이 있는걸요 쨌든 삼각형에 직각이 부분적으로 없다고 직각삼각형 아니다라고 선언하는건 사실 완전틀리긴하죠
|
||||||||||||||